Decoding Linear Soft SVM for Classification over Linear Hard SVM
Machine Learning Classification Algorithms
Table Of Contents :

Motivation
While devising the SVM algorithm, we did not mention it explicitly but we inherently took a linearly separable dataset, but what if the dataset is not linearly separable (also called overlapping class dataset) and yet you want to apply ‘Linear’ SVM?? Will ‘Linear’ SVM work?


Solution
In Linear Hard SVM we did not allow any mis-classifications i.e. inside the margin there were no data points, but here the idea is that we will allow some misclassifications (hence called SOFT), and hence some data points will be visible inside the margin, as can be seen in below diagram !!
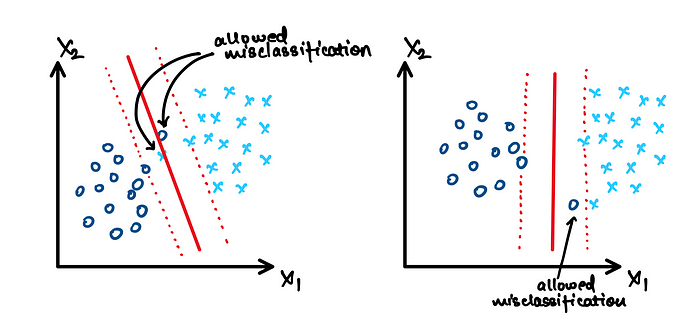

Mathematical Formulation



PRIMAL Optimization Equation Formulation
Hence the primal optimization equation derived in Linear Hard SVM changes as follows for Linear Soft SVM


Now let us understanding the effect of Regularization done in above optimization equation !!


Solving the Optimization Equation by converting it from PRIMAL to its DUAL form
Now as we saw earlier in Hard SVM, we will solve further by converting this primal problem into its dual form




Intuitively it means that in Hard Margin SVM we did not have any upper bound for lamdas but here in Soft Margin SVM we have an upper bound and that upper bound is nothing but the regularization term ‘apha’

Solving Dual Optimization Problem
Now the above dual optimization problem is also a constrained non-linear optimization problem and more specifically it is a convex quadratic programming problem (QPP). There are many was to solve this kind of convex QPP based dual problem, one of the most famous algorithm to solve is using SMO algorithm. Using this algorithm you will find optimal values of lambdas….


Now let’s again go to the original question i.e. how to calculate W0', you can use the same trick that you used in hard SVM i.e. use support vector to calculate W0' (either any of of the support vector or use all and then averge it)

Hinge Loss Derivation
Above we saw primal optimization problem formulation i.e.

This can be re-written as follows


Hence on substituting it back into the equation, we get


